Subtraction Strategies
Students, as we conclude our subtraction unit, should be comfortable with multiple subtraction strategies. Solving a problem in using two strategies prevents a computational error that may have been overlooked. Our goal is to have students who can recognize, based on the situation, the most efficient strategy with the least likelihood of error, and with the idea that mental math can be one of the most effective ways to solve.
For example, we don’t want students to use the traditional algorithm to solve an equation like 1000-989=m, because it would be easy for them to make a computational error when regrouping multiple times. Rather, we want students to recognize that the distance between these two numbers can easily be done by counting up, 989+1=990 and 990+10=1000,therefore, the difference is 11.
Of course, in other situations, it's simply easier to solve using the traditional algorithm. In 876-563, the quickest way to the difference is simply using the traditional algorithm.
In order to develop number flexibility, we’ve been working on several strategies in class.
Sample Problem: 245 - 178 = m
Adding up
Turn
the equation into a missing addend 178 + m = 245. Put the number 178 on a
number line and count up to the next landmark number. (Landmark numbers
have a O or 5 in the ones place.) 178 count up 2 to 180, count up 20 to 200, and then jump 45 from 200 to 245. Adding the jumps gives you the answer, m = 67.
Decomposing
Decomposing
Decompose
the number by place value, then subtract each place value. In this problem, 200-100 = 100, 40-70 =
-30, 5-8 = -3, therefore 100-30-3= 67. Sometimes, this strategy has
you in negative numbers, but students know that 0 is the middle of the
number system and can flexibly use negative numbers. Some students use
this strategy and regroup from the larger place value. If they did that
in this problem, they would take a group of 100 from 200 and put 140 in
the tens place.
245 : 200 + 40 + 5
-178 : -100 + 70 + 8
100 - 30 - 3 = 67
Counting backward
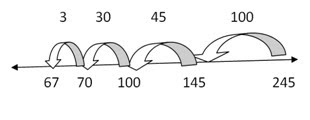
245 - 178 = m
Put 245 on the open number line and count backward 178. You can make the jump of 178 any way you want. Most kids jump backward to landmark numbers. 245 jump back 45 is 100, and then jump back 30 is 70, then jump back 3 is 67. This strategy works best for students who can readily count backward, other students find it difficult.
Put 245 on the open number line and count backward 178. You can make the jump of 178 any way you want. Most kids jump backward to landmark numbers. 245 jump back 45 is 100, and then jump back 30 is 70, then jump back 3 is 67. This strategy works best for students who can readily count backward, other students find it difficult.
Left to Right
Students think 200 – 100 = 100 and 40 – 70 = -30 and 5 – 8 = -3. Then, 100-30 is 70, and 70-3 is 67.
245 :
-178 :
100 – 30 – 3
70 – 3 = 67
Compensation / Creating an Equivalent Problem
In
some situations, we also encourage students to compensate to create an
easier equivalent problem. Generally, in subtraction, when you create an
equivalent problem your goal is to create a problem where regrouping is
not necessary. Many students try to create the digit 9 in their
minuend.
For example,
56 + 3 59
-47 -3 -44
15
Remember, the purpose of exposing students to multiple strategies is two-fold. First, students need to be able to solve using two different strategies to check their work, and secondly students will be able to identify the strategy that is most efficient based on the problem. Students who successfully accomplish this have number sense and are able to work with numbers mentally and flexibly. Our students are busy every day becoming young mathematicians.

No comments:
Post a Comment