If you ask me what I'm passionate about, it's teaching students to embrace a love of mathematics, see themselves as young mathematicians, and build a number sense that will allow them to think flexibly about numbers. Teaching math to children, for me, is second nature.
Science, on the other hand, isn't my forte'. So, I find myself working overtime trying to compensate for what I see as my weaker content area. These kids deserve the the best so though it's not my strength, I must remember it may be their passion. I must, as their teacher, show the same level of competence and enthusiasm for the subject that doesn't come as easily to me. So, as you can imagine, it takes a tremendous amount of planning and preparation, and professional reading on my part to make sure that I offer an engaging science laboratory for my students. I hope that as I'm building young mathematicians, I am also building young scientists.
My goal this year was to plan more hands on experiences. I'm aiming for one a week and so far, I've been pretty successful. The post below is from our lab this week.
 Today, our young scientists were busy at work in their laboratory. They were seeking the answer to their essential question, How can the pull of gravity be overcome?
They were given a hairdryer, three ping pong balls, and a cotton ball.
Their task was to set the hair dryer on cool, point it toward the
ceiling, and then carefully put a ping pong ball in the stream of air.
Today, our young scientists were busy at work in their laboratory. They were seeking the answer to their essential question, How can the pull of gravity be overcome?
They were given a hairdryer, three ping pong balls, and a cotton ball.
Their task was to set the hair dryer on cool, point it toward the
ceiling, and then carefully put a ping pong ball in the stream of air.
They concluded that the force of air was stronger than the pull of
gravity so the ping pong ball floated in the air stream. Then, they
turned the hair dryer slightly to the left and slightly to the right,
and noticed that the ping pong ball would follow the air stream and stay
suspended, unless, like one group discovered, the stream of air was not
strong enough. In that case, the pull of gravity would be stronger and
the ping pong ball would be pulled toward Earth.
Next, the young scientists tried floating two or more ping pong balls in
the air stream. Some groups were successful while others were not. The
discussion behind the mixed results provided an excellent way to
introduced the independent variables (What changed?), dependent
variables (What did not change?), and constants in this hands on lab.
In addition, the students discovered that floating the cotton ball had a
different result. In their exploration, they also discovered that the
cotton ball would stick to the bottom of the hairdryer and stop the flow
of air.
When this occurred, the forced air would be weaker than the
pull of gravity.

In
our analysis of the lab, students quickly made the connection that the
air stream was stronger than the pull of gravity on the mass of the ping
pong ball. (Actually, they even strengthened their understanding the following day after a video clip and a reading that the two forces were in balance and that's why the ball levitates in mid-air.)
We asked, "What do you think would happen if we tried the
same thing with a golf ball or even a basketball?" Students concluded
that the mass of the golf ball and basketball would be too much for the
air stream and gravity would pull it to the ground. However, they also
recognized that with a great enough force, they would be able to get the
golf ball and basketball to levitate. Some students thought that a leaf
blower would work to levitate heavier objects.
In Closing, one student shared that he once was in a machine that made
him levitate! He's bringing a video of the experience in for the class
to see. How exciting!
Today's lab explored Bernoulli's Principle, the principle that
allows heavier-than-air objects like airplanes to fly. Bernoulli
discovered that the faster air flows over an object, the less the air
pushes on the surface of the object and so the lower the pressure. In
this lab, gravity is pulling on the ball while the pressure from the
forced air pushes up on the ball. The forces are balanced,so the ball
hovers in the air. You can move the hair dryer from side to side, and
the ball will stay hovering in mid-air until one of the forces is
stronger than the other.
The students loved the lab and the learning was evident. We hope your
young scientist shared their enthusiasm. Furthermore, if you are a
student reading this post, we'd love it if you leave us a comment and
tell us what you liked most about today's gravity lab.














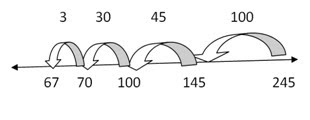
 This
understanding is extremely important as students move into problems
that are more difficult when they begin multiplication like 6x8. When in
the early stages of developing automaticity, they may not know 6x8, but
if they know (3x8), they can solve 2(3x8), or, if they know 6x4, they
can solve 2(6x4).
This
understanding is extremely important as students move into problems
that are more difficult when they begin multiplication like 6x8. When in
the early stages of developing automaticity, they may not know 6x8, but
if they know (3x8), they can solve 2(3x8), or, if they know 6x4, they
can solve 2(6x4). Students’
ability to think flexibly with decomposing arrays in multiple ways,
builds a strong foundation for fluency in multiplication. The skill
allows students to attack any multiplication equation for which they
don’t automatically have a product, and leads into being able to solve
more difficult equations like 14 x 12.
Students’
ability to think flexibly with decomposing arrays in multiple ways,
builds a strong foundation for fluency in multiplication. The skill
allows students to attack any multiplication equation for which they
don’t automatically have a product, and leads into being able to solve
more difficult equations like 14 x 12.